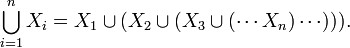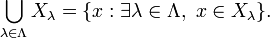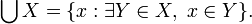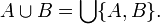Union (set theory)

In set theory, union (denoted as ∪) is a set operation between two sets that forms a set containing the elements of both sets.

Formally, the union A ∪ B is defined by the following: a ∈ A ∪ B if and only if ( a ∈ A ) ∨ ( a ∈ B ), where ∨ - is logical or. We see this connection between ∪ and ∨ symbols.

Contents 1 Properties 2 General unions 2.1 Finite unions 2.2 Infinite unions 3 See also 4 References

Properties

The union operation is:

• associative - (A ∪ B) ∪ C = A ∪ (B ∪ C)
• commutative - A ∪ B = B ∪ A.

General unions

Finite unions

The union of any finite number of sets may be defined inductively, as

Infinite unions

The union of a general family of sets X_λ as λ ranges over a general index set Λ may be written in similar notation as

We may drop the indexing notation and define the union of a set to be the set of elements of the elements of that set:

In this notation the union of two sets A and B may be expressed as

See also

• Disjoint union
• Intersection

References

• Paul Halmos (1960). Naive set theory. Van Nostrand Reinhold.  Section 4.
• Keith J. Devlin (1979). Fundamentals of Contemporary Set Theory. Springer-Verlag, 5,10. ISBN 0-387-90441-7. 

Some content on this page may previously have appeared on Citizendium.