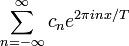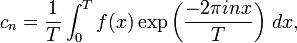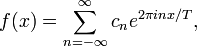Fourier series
From Knowino
In mathematics, the Fourier series, named after Joseph Fourier (1768—1830), of a complex-valued periodic function f of a real variable, is an infinite series
defined by
where T is the period of f.
In what sense it may be said that this series converges to f(x) is a somewhat delicate question. However, physicists being less delicate than mathematicians in these matters, simply write
and usually do not worry too much about the conditions to be imposed on the arbitrary function f(x) of period T for this expansion to converge to it.
| |
Some content on this page may previously have appeared on Citizendium. |