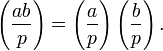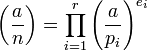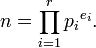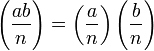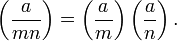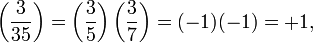Quadratic residue
In modular arithmetic, a quadratic residue for the modulus N is a number which can be expressed as the residue of a2 modulo N for some integer a. A quadratic non-residue of N is a number which is not a quadratic residue of N.
Contents |
Legendre symbol
When the modulus is a prime p, the Legendre symbol  expresses the quadratic nature of a modulo p. We write
expresses the quadratic nature of a modulo p. We write
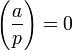 if p divides a;
if p divides a;
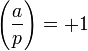 if a is a quadratic residue of p;
if a is a quadratic residue of p;
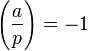 if a is a quadratic non-residue of p.
if a is a quadratic non-residue of p.
The Legendre symbol is multiplicative, that is,
Jacobi symbol
For an odd positive n, the Jacobi symbol  is defined as a product of Legendre symbols
is defined as a product of Legendre symbols
where the prime factorisation of n is
The Jacobi symbol is bimultiplicative, that is,
and
If a is a quadratic residue of n then the Jacobi symbol 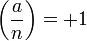 , but the converse does not hold. For example,
, but the converse does not hold. For example,
but since the Legendre symbol 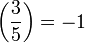 , it follows that 3 is a quadratic non-residue of 5 and hence of 35.
, it follows that 3 is a quadratic non-residue of 5 and hence of 35.
See also
References
- G. H. Hardy; E. M. Wright (2008). An Introduction to the Theory of Numbers, 6th ed. Oxford University Press. ISBN 0-19-921986-9.
| |
Some content on this page may previously have appeared on Citizendium. |