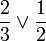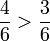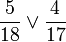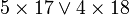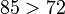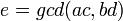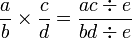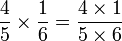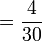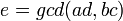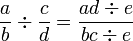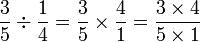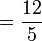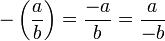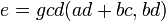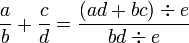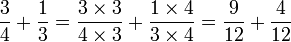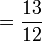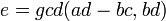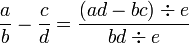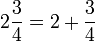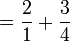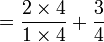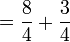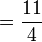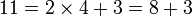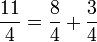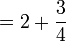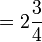Fraction (mathematics)
In mathematics, a fraction (from the Latin fractus, meaning broken) is a concept used to convey a proportional relation between a part and the whole. It consists of a numerator (an integer — the part) and a denominator (a natural number — the whole). For instance, the fraction  can represent three equal parts of a whole object, if the object is divided into five equal parts. Any rational number can be written as a fraction.
can represent three equal parts of a whole object, if the object is divided into five equal parts. Any rational number can be written as a fraction.
Fractions are a special case of ratios. For instance, 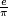 is a valid ratio, but it is not a fraction since we cannot compute an equivalent fraction with an integer numerator and a natural number denominator. A fraction with equal numerator and denominator is equal to one (e.g.,
is a valid ratio, but it is not a fraction since we cannot compute an equivalent fraction with an integer numerator and a natural number denominator. A fraction with equal numerator and denominator is equal to one (e.g., 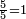 ). Because the division by zero is undefined, zero should never be the denominator of a fraction.
). Because the division by zero is undefined, zero should never be the denominator of a fraction.
Due to tradition and conventions, there are at least two ways to write a fraction. The numerator and the denominator may be separated by a slash (e.g., 3/4), or by a vinculum (e.g.,  ). Since we can compute the quotient from a fraction, we can represent any fraction with a decimal numeral (e.g.,
). Since we can compute the quotient from a fraction, we can represent any fraction with a decimal numeral (e.g., 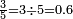 ).
).
In higher mathematics, a fraction is viewed as an element of a field of fractions, the smallest field of the integral domain.
Contents |
Forms
A vulgar fraction (or common fraction) simply refers to a numerator divided by a denominator (e.g., 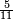 and
and 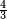 ). It is said to be a proper fraction if the absolute value of the numerator is less than the denominator (usually assumed positive, otherwise its absolute value is relevant here); e.g.
). It is said to be a proper fraction if the absolute value of the numerator is less than the denominator (usually assumed positive, otherwise its absolute value is relevant here); e.g. 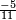 . An improper fraction (in the United Kingdom, top-heavy fraction) is said if the absolute value of the numerator is greater than or equal to the denominator (e.g.
. An improper fraction (in the United Kingdom, top-heavy fraction) is said if the absolute value of the numerator is greater than or equal to the denominator (e.g. 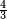 ). All integers different from -1, 0, and 1 can be represented by an improper fraction, since for example
). All integers different from -1, 0, and 1 can be represented by an improper fraction, since for example 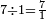 . The 1 at the denominator is sometimes called an "invisible denominator".
. The 1 at the denominator is sometimes called an "invisible denominator".
A mixed number is the sum of an integer and a proper fraction (e.g., 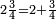 ). An improper fraction can be transformed into a mixed number and vice-versa.
). An improper fraction can be transformed into a mixed number and vice-versa.
Special cases
- A vulgar fraction with a numerator of 1, e.g.
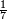 , is a unit fraction.
, is a unit fraction.
- An Egyptian fraction is the sum of distinct unit fractions, e.g.
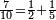 .
.
- A decimal fraction is a vulgar fraction in which the denominator is a power of ten, e.g.
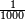 .
.
- A dyadic fraction is a vulgar fraction in which the denominator is a power of two, e.g.
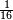 .
.
- An expression that has the form of a fraction but actually represents division by or into an irrational number is sometimes called an "irrational fraction". A common example found in trigonometry is
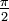 , the measure of a right angle in radians.
, the measure of a right angle in radians.
- A complex fraction (or compound fraction) is a fraction in which the numerator and denominator contain a fraction (e.g.,
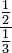 ). To simplify, divide the numerator by the denominator.
). To simplify, divide the numerator by the denominator.
- A continued fraction is an expression such as
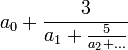 , where the
, where the 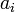 are integers.
are integers.
- Rational functions are represented in the form of a fraction, where the numerator and denominator are polynomials. They are the quotient field of the polynomials.
- In algebra, some rational expressions (a fraction with an algebraic expression in the denominator) are written as the sum of other rational expressions with denominators of lesser degree. For instance, the rational expression
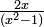 can be rewritten as the sum of two fractions :
can be rewritten as the sum of two fractions : 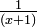 and
and 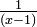 . The decomposition is made of partial fractions.
. The decomposition is made of partial fractions.
Notation
There are many equivalent notations for a fraction.
The numerator and the denominator may be separated by a slanted line, the slash or the solidus (e.g., 3/4), or by an horizontal line, the vinculum (e.g.,  ). In some contexts (like road signs in some countries), it is clear that two numerals are the numerator and the denominator. They are written without any separator : a b (e.g., 3 4). The colon separator is usually found in written ratios (e.g., 1.5 : 2 = 3 : 4). The "÷" symbol is sometimes used to express a fraction (e.g., 3 ÷ 4), but should not.
). In some contexts (like road signs in some countries), it is clear that two numerals are the numerator and the denominator. They are written without any separator : a b (e.g., 3 4). The colon separator is usually found in written ratios (e.g., 1.5 : 2 = 3 : 4). The "÷" symbol is sometimes used to express a fraction (e.g., 3 ÷ 4), but should not.
Percentages ("%") allow to write a numeral as a fraction, the denominator being implicitly 100 (e.g., 14.5% = 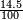 ). Per mills ("‰") allow to write a numeral as a fraction, the denominator being implicitly 1,000 (e.g., 22.3‰ =
). Per mills ("‰") allow to write a numeral as a fraction, the denominator being implicitly 1,000 (e.g., 22.3‰ = 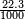 ). Per cent mille (pcm) allow to write a numeral as a fraction, the denominator being implicitly 100,000 (e.g., 78.7 pcm =
). Per cent mille (pcm) allow to write a numeral as a fraction, the denominator being implicitly 100,000 (e.g., 78.7 pcm = 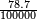 ). Parts per million (ppm), parts per billion (ppb) and parts per trillion (ppt) are others way to write a numeral as a fraction with the implicit denominators 1 million, 1 billion, and 1 trillion.
). Parts per million (ppm), parts per billion (ppb) and parts per trillion (ppt) are others way to write a numeral as a fraction with the implicit denominators 1 million, 1 billion, and 1 trillion.
In pie charts, any portion convey the proportional relation between a part and the whole.
|
A fraction is sometimes represented by a rectangular grid. We could represent |
|
Arithmetic operations
The most common arithmetic operations on fractions are addition, subtraction, multiplication, and division. When adding and subtracting, we must often compute the equivalent fractions. When dividing, we usually compute the multiplicative inverse. After any computation, the end result should be an irreducible fraction.
In this section, each subsection builds upon knowledge acquired in previous subsections. For instance, the addition subsection does not come before the multiplication subsection, since fraction addition usually involves fraction multiplication.
Any integer can be represented by a fraction (e.g., 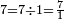 and
and 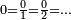 ). Thus, if an operation is applied to an integer and a fraction, convert the integer into a fraction and apply the appropriate algorithm.
). Thus, if an operation is applied to an integer and a fraction, convert the integer into a fraction and apply the appropriate algorithm.
For the remainder of this section, it is understood that  and
and  .
.
Equivalent fractions
Multiplying (or integer dividing) the numerator and the denominator of a fraction by the same non-zero integer results in a new fraction that is said to be equivalent to the original fraction. For instance, 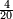 and
and  are equivalent, since
are equivalent, since 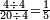 .
.
A fraction where the numerator and the denominator do not have any common factor, 1 excepted, is said irreducible (or in its lowest terms). If it is not the case, then divide its numerator and its denominator by their gcd. For instance, 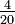 is not in lowest terms because both 4 and 20 can be exactly divided by 4, giving
is not in lowest terms because both 4 and 20 can be exactly divided by 4, giving 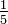 . In contrast,
. In contrast, 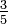 is in lowest terms.
is in lowest terms.
Comparison
To compare fractions with different denominators, find their equivalent fraction with the same denominator. The fraction with highest numerator is the greatest.
For instance, is 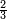 greater than
greater than 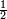 ?
?
The "cross-multiply" method say to multiply the top and bottom numbers crosswise. The product of the denominators is used as a common (but not necessary the least common) denominator. The highest numerator identifies the largest fraction. Since both denominators are the same, they can be dropped.
For instance, is 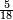 greater than
greater than 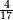 ?
?
Multiplication
Formally, apply this algorithm to multiply the fractions 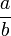 and
and 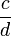 :
:
By hands, the multiplication is done like this.
- For the resulting fraction,
- Set its numerator to the product of both numerators.
- Set its numerator to the product of both denominators.
- Reduce the resulting fraction if you need to.
For instance, what is the result of 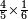 ?
?
Since the result is not an irreducible fraction, we may reduce it. We divide the numerator and the denominator by their gcd, 2 :
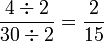 .
.
Multiplicative inverse
The multiplicative inverse of a fraction is :
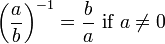 .
.
Division
Dividing by a fraction is the same as multiplying by its inverse.
Formally, apply this algorithm to divide the fractions 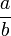 and
and 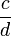 :
:
By hands, the division is done like this.
- Exchange the numerator and the denominator in the second fraction (equivalent to computing the multiplicative inverse).
- For the resulting fraction,
- Set its numerator to the product of both numerators.
- Set its numerator to the product of both denominators.
- Reduce the resulting fraction if you need to.
For instance, what is the result of 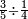 ?
?
The result is an irreducible fraction.
Additive inverse
The additive inverse of a fraction is :
Addition
Formally, apply this algorithm to add the fractions 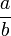 and
and 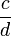 :
:
By hands, the addition is done like this.
- Compute an equivalent fraction of
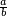 and
and 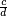 , making sure both have the same denominator.
, making sure both have the same denominator.
- For the resulting fraction,
- Set its numerator to the addition of the numerators.
- Set its denominator to the computed denominator (the three fractions have the same denominator).
- Reduce the resulting fraction if you need to.
For instance, what is the result of 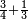 ?
?
Let's find a number that both denominators will divide : It is 12. We are ready to compute the equivalent fractions :
This is the final answer since it is an irreducible fraction.
Subtraction
Formally, apply this algorithm to subtract the fractions 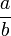 and
and 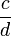 :
:
By hands, the subtraction is done like this.
- Compute an equivalent fraction of
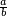 and
and 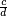 , making sure both have the same denominator.
, making sure both have the same denominator.
- For the resulting fraction,
- Set its numerator to the subtraction of the numerators.
- Set its denominator to the computed denominator (the three fractions have the same denominator).
- Reduce the resulting fraction if you need to.
Since this algorithm is very similar to the addition algorithm, we do not give any example.
Mixed numerals
A mixed numeral has the form 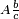 , where A is the integer part and
, where A is the integer part and 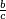 is the fractional part. Implicitly, there is a plus symbol between the parts (e.g.,
is the fractional part. Implicitly, there is a plus symbol between the parts (e.g., 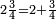 ).
).
Just like any fraction, we can add, subtract, multiply, and divide mixed numerals. However, before applying the operation, convert the mixed numeral to improper fraction, or there can be wrong results.
For instance, what is the sum of 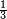 and
and 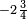 ? The minus sign applies also to the fractional part
? The minus sign applies also to the fractional part  :
: 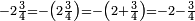 . The answer is
. The answer is 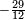 or
or 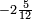 .
.
Mixed numeral to improper fraction
A mixed numeral can be converted to an improper fraction with this algorithm :
- Insert a plus symbol between the integer and the fraction.
- Replace the integer with its equivalent fraction on 1.
- Add both fractions.
For instance, transform 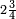 to an improper fraction.
to an improper fraction.
Improper fraction to mixed numeral
An improper fraction can be converted to a mixed numeral with this algorithm :
- Integer divide the numerator by the denominator.
- The quotient becomes the whole part and the remainder becomes the numerator of the fractional part.
- The fraction has the same denominator.
For instance, transform 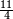 to a mixed number.
to a mixed number.
Decimal numerals
A decimal numeral has the form 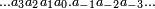 , where the
, where the 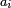 are base ten digits (0, 1, 2,... 9).
are base ten digits (0, 1, 2,... 9).
Fraction to decimal numeral
To get the equivalent decimal numeral of a fraction, divide the numerator by the denominator (e.g., 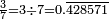 ).
).
Decimal numeral to fraction
In many cases, it is easier to work with decimal numerals, but they lack precision compared to fractions. Sometimes an infinite number of decimals is required to convey the same precision. Thus, it is often useful to convert decimal numerals into fractions.
Before going any further in this section, we need to observe a property of the decimal numerals. For instance, 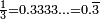 The infinite expansion is composed of 3s. For square root of 2, we have
The infinite expansion is composed of 3s. For square root of 2, we have 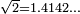 . The infinite expansion is composed of different digits without any repeated pattern. For 4.35, we have
. The infinite expansion is composed of different digits without any repeated pattern. For 4.35, we have 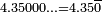 The infinite expansion is composed of zeroes, but they are not written down by convention. Thus, all numbers written in decimal notation have an infinite decimal expansion.
The infinite expansion is composed of zeroes, but they are not written down by convention. Thus, all numbers written in decimal notation have an infinite decimal expansion.
Because of this observation, we only need to use two algorithms to convert decimal numerals to fractions. In order to choose the appropriate algorithm, we need to find if there is a repeating pattern, or not, in the decimal expansion.
Repeating pattern algorithm
The idea behind the following algorithm is to compute two different multiples of the same number in such a way as to align the repeated pattern after the decimal separator.
- Excluding any repeated pattern, count the number of digits after the decimal separator (p) in the decimal numeral n.
- Compute
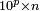
- Including the first repeated pattern, count the number of digits after the decimal separator (q) in the decimal numeral n.
- Compute
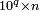
- Write the equation
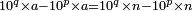 , where a is unknown.
, where a is unknown.
- Isolate a, the fraction to find.
For instance, convert 7.85891891891... to a fraction.
- m is equal to 2
- 102 = 100
- 7.85891891891... × 100 = 785.891891891...
- n is equal to 5
- 105 = 100000
- 7.85891891891... × 100000 = 785891.891891...
- 100000 × a - 100 × a = 785891.891891... - 785.891891891...
- 99900 × a = 785106
-
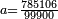
- ...
For instance, convert 4.37 to a fraction.
- m is equal to 2.
- 102 = 100
- 4.37000... × 100 = 437.000...
- n is equal to 3.
- 103 = 1000
- 4.37000... × 1000 = 4370.00...
- 1000 × a - 100 × a = 4370.00... - 437.000...
- 900 × a = 3933
-
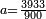
- ...
Non-repeating pattern algorithm
The conversion is done using observation and needs.
If the decimal numeral n is a multiple of 3.14159 (a truncated value of π), then solve 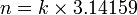 , where k is the multiple to find. If the constant is unknown, then truncate the decimal expansion to needed precision. Convert the new numeral using repeating pattern algorithm.
, where k is the multiple to find. If the constant is unknown, then truncate the decimal expansion to needed precision. Convert the new numeral using repeating pattern algorithm.
History
Ancient Egyptians used what is called today Egyptian fractions. In China, they were in use around the first century of our era.
Some problems from Antiquity explicitly request fraction use :
- I found a stone, but I did not weigh it. After adding a seventh of its weight and added the eleventh of the new result, it weighs 1 ma-na [mass unit]. What is the stone weight ? (Babylonian problem, tablet YBC 4652, problem 7)
- A number added to its seventh gives 19. What is the number ? (Rhind Mathematical Papyrus, problem 24)
- A number added to its quarter gives 15. What is the number ? (Rhind Mathematical Papyrus, problem 26)
- Suppose we have 9 golden rods and 11 white silver rods which, when they are weighed, have exactly the same weight. If we replace one golden rod with one white silver rod, gold is ligther by 13 liang [mass unit]. What is the weight of one golden rod and of one white silver rod ? (The Nine Chapters on the Mathematical Art, problem 7.17)
Historically, any numeral that did not represent a whole number was called a "fraction". The numerals that we now call "decimals" were originally called "decimal fractions"; the numeral we now call "fractions" were called "vulgar fractions", meaning a "commonplace fraction".
See also
| |
Some content on this page may previously have appeared on Citizendium. |

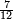 by this grid :
by this grid :