Closed set
From Knowino
In mathematics, a set 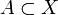 , where (X,O) is some topological space, is said to be closed if its complement in X, the set
, where (X,O) is some topological space, is said to be closed if its complement in X, the set 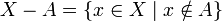 , is open. The empty set and the set X itself are always closed sets. The finite union and arbitrary intersection of closed sets are again closed.
, is open. The empty set and the set X itself are always closed sets. The finite union and arbitrary intersection of closed sets are again closed.
Examples
-
Let X be the open interval (0, 1) with the usual topology induced by the Euclidean distance. Open sets are then of the form
![\bigcap_{\gamma \in \Gamma} (0,a_{\gamma}]\cup [b_{\gamma},1).](images/math/0/d/e/0ded9faeafcded66cb462899aaa2ee37.png) .
.
-
As a more interesting example, consider the function space C[a,b] (with a < b). This space consists of all real-valued continuous functions on the closed interval [a, b] and is endowed with the topology induced by the norm
| |
Some content on this page may previously have appeared on Citizendium. |
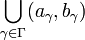
![\|f\| = \max_{x \in [a,b]} |f(x)|.](images/math/d/8/a/d8a6bd2a702ef2aa746bb6cfa77f9f62.png)
![A = \big\{ f \in C[a,b] \mid \min_{x \in [a,b]} f(x) > 0 \}](images/math/1/9/c/19c104d304f8c8491dca6329db57e836.png)
![B = \big\{ f \in C[a,b] \mid \min_{x \in [a,b]} f(x) < 0 \}](images/math/9/b/2/9b2ac15a32e79108c0cdf2f141b31b0f.png)
![C = \big\{ f \in C[a,b] \mid \min_{x \in [a,b]} f(x) \ge 0 \}](images/math/0/9/2/0929b9ab1f6bf04c0e1c892f7840a174.png)
![D = \big\{ f \in C[a,b] \mid \min_{x \in [a,b]} f(x) \le 0 \}](images/math/e/6/d/e6dd9f6a73734279530f6657f5cb70cb.png)