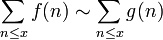Average order of an arithmetic function
From Knowino
This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 14 January 2011.
In mathematics, in the field of number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".
Let f be a function on the natural numbers. We say that the average order of f is g if
as x tends to infinity.
It is conventional to assume that the approximating function g is continuous and monotone.
Examples
- The average order of d(n), the number of divisors of n, is log(n);
- The average order of σ(n), the sum of divisors of n, is
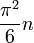 ;
;
- The average order of φ(n)), Euler's totient function of n, is
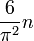 ;
;
- The average order of r(n)), the number of ways of expressing n as a sum of two squares, is π ;
- The Prime Number Theorem is equivalent to the statement that the von Mangoldt function Λ(n) has average order 1.
See also
References
- G.H. Hardy; E.M. Wright (2008). An Introduction to the Theory of Numbers, 6th ed.. Oxford University Press, 347-360. ISBN 0-19-921986-5.
- Gérald Tenenbaum (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press, 36-55. ISBN 0-521-41261-7.
| |
Some content on this page may previously have appeared on Citizendium. |