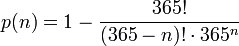Birthday paradox
The birthday paradox or, more modestly, the birthday problem (sometimes also the birthday coincidence) is the following — at least on first glance — surprising result of probability theory:
- For any group of 23 or more people, it is more likely than not that there are two persons who have their birthday anniversary on the same date.
- Moreover, if there are more than 60 people, then it is even almost certain that such a pair exists (more precisely, on average 99 out of a 100 groups will include at least one such pair).
This problem was introduced and discussed in the 1930s when modern probability theory emerged and is often attributed to Richard von Mises.
Generalized versions of the birthday paradox have applications in cryptography, whenever two things to turn out coincidentally the same is an issue (birthday attack).
Remark:
This statement is not a true paradox in its logical sense.
Nevertheless the term is traditionally used because of the counterintuitive nature of this result.
Probabilistic calculation
- In this article leap years and other details (such as a difference between winter and summer days) are ignored.
To show how to calculate the probability of a group including such a match, it is simpler to first find the probability of all the birthdays being different. Consider a group of two people. The first person can have been born on any of the 365 days of the year, while the second must have been born on one of the other 364 days in order to not match. For the first person alone, a match cannot happen, thus the no-match probability is 1, which is 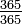 in the sense that all the 365 possibilities lead to no-match. Given the first person's birthday, the second person's birthday differs in 364 cases, with a conditional probability of
in the sense that all the 365 possibilities lead to no-match. Given the first person's birthday, the second person's birthday differs in 364 cases, with a conditional probability of 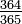 which is 0.9973. Multiplying these probabilities together gives a net (unconditional) probability of 0.9973 for having different birthdays. Subtracting this number from 1.0 gives a 0.0027 probability of having the same birthday.
which is 0.9973. Multiplying these probabilities together gives a net (unconditional) probability of 0.9973 for having different birthdays. Subtracting this number from 1.0 gives a 0.0027 probability of having the same birthday.
The third person in the group, having to miss the birthdays of the first two people, has only 363 days, with a probability of 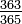 which is 0.9945. Multiplying this on to the previous result, gives 0.9918.
which is 0.9945. Multiplying this on to the previous result, gives 0.9918.
For four in the group, the probability of a pair matching birthdays is 1 − 0.9836 = 0.0164, over 1 percent.
The formula for the probability of having a matching birthday in a group of n people is
As more and more people come into the group, the number of nonmatching days available decreases; and the probability of everyone having a different birthday decreases. Thus the probability of there being two with the same birthday increases. Continuing to multiply more and more, smaller and smaller fractions, a point near 0.5 is exceeded as soon as the group consists of 23 people.
The data below shows that as the size of the group grows, the probability of having a match increases very quickly.
| N | p(n) |
|---|---|
| 5 | 0.0271 |
| 10 | 0.1170 |
| 15 | 0.2529 |
| 20 | 0.4114 |
| 22 | 0.4757 |
| 23 | 0.5073 |
| 25 | 0.5687 |
| 30 | 0.7063 |
| 40 | 0.8912 |
| 50 | 0.9704 |
| 60 | 0.9941 |
| 70 | 0.9992 |
| 80 | 0.9999 |
So in a group of 80 people, only one time in ten thousand will everyone have a different birthday.
| |
Some content on this page may previously have appeared on Citizendium. |