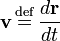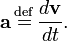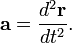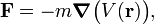Acceleration
In common parlance, the acceleration of an object is the increase of its speed per unit time (say, per second); a decrease in speed is usually called deceleration. In physics one speaks in these cases of positive and negative acceleration.
Speed is a single real number, the ratio of length and time, while velocity and acceleration are vectors (have length and direction). In physics, the vector acceleration is defined as a change in the vector velocity. Such a change can be in the length of the velocity vector, i.e., in the speed of the object, or in the direction of the velocity vector, or in both at once. For instance, an object traveling at constant speed in a circular pattern (making a fixed number of cycles per second) is undergoing acceleration due to the continuous change in the direction of velocity.
Contents |
[edit] Physics definition of acceleration
In physics, speed is the absolute value (magnitude) of velocity, a vector. Physicists define the velocity of a point in space as the derivative of the position-vector of the point with respect to time. Conventionally, the position of a point is designated by r (a vector), velocity by v, acceleration (a vector) by a, and time by t (a scalar). Hence,
and the acceleration a is the derivative of v with respect to time,
Accordingly, acceleration is the second derivative of the position of a point in space with respect to time,
The direction and length of a may vary from one instant to the other. Since it is not meaningful to compare two non-parallel vectors, the term deceleration is hardly ever used in physics. The second derivative of r with respect to time, whatever its magnitude or direction, is referred to as acceleration. The unit of acceleration is length per time squared (in SI: m s−2).
[edit] Acceleration of a body
If the object is not a point, but a body of finite extent, we recall that the motion of the body can be separated in a translation of the center of mass and a rotation around the center of mass. The definitions just given then apply to the position r of the center of mass and the translational velocity and translational acceleration of the center of mass of the body.
The rotational motion of the body is somewhat more difficult to describe. In particular one can prove that there cannot exist in three dimensions a set of angular coordinates such that their first derivative with respect to time is the angular velocity, see rigid rotor for more details. Accordingly, angular acceleration cannot be given as second derivatives of some coordinates with respect to time (except for the special case of rotation around an axis fixed in space).
[edit] Relation to force
One of the fundamental laws of physics is Newton's second law. This states that the acceleration of the center of mass of a (rigid) body is proportional to the force acting on the body. The relation between force and acceleration being linear, the proportionality constant is a property of the body only; it is the mass of the body.
In classical mechanics it is frequently the case that the force on a body is proportional to the gradient ∇ of a potential V,
with m the total mass of the body.[1] Comparing with Newton's second law, we see that −∇ V is the acceleration of the body (provided m∇V is the only force operative on the body). An example of an acceleration due to a potential is the acceleration due to gravity.
[edit] Note
- ↑ A force equal to minus the gradient of a potential is non-dissipative. Friction is an example of a dissipative force.
| |
Some content on this page may previously have appeared on Citizendium. |