Denseness

In mathematics, denseness is an abstract notion that captures the idea that elements of a set A can "approximate" any element of a larger set X, which contains A as a subset, up to arbitrary "accuracy" or "closeness".

Formal definition

Let X be a topological space. A subset 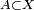is said to be dense in X, or to be a dense set in X, if the closure of A coincides with X (that is, if 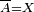); equivalently, the only closed set in X containing A is X itself.

Examples

1. Consider the set of all rational numbers 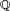. It can be shown that for an arbitrary real number a and desired accuracy 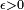, one can always find some rational number q such that 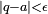. Hence the set of rational numbers is dense in the set of real numbers ()
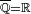2. The set of algebraic polynomials can uniformly approximate any continuous function on a fixed interval [a,b] (with b>a) up to arbitrary accuracy. This is a famous result in analysis known as Weierstrass' theorem. Thus the algebraic polynomials are dense in the space of continuous functions on the interval [a,b] (with respect to the uniform topology).

Some content on this page may previously have appeared on Citizendium.