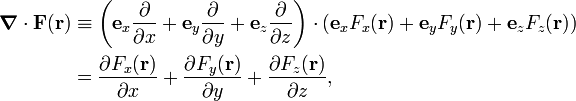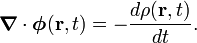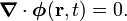Divergence
In vector analysis, the divergence of a differentiable vector field F(r) is given by an expression involving the operator nabla (∇)—also known as the del operator. The definition of nabla and divergence are given by the following equations:
where ex, ey, ez form an orthonormal basis of 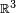 . The dot stands for a dot product. In the older literature one finds the notation div F for ∇⋅F.
. The dot stands for a dot product. In the older literature one finds the notation div F for ∇⋅F.
Physical meaning
The physical meaning of divergence is given by the continuity equation. Consider a compressible fluid (gas or liquid) that is in flow. Let φ(r,t) be its flux (mass per unit time passing through a unit surface) and let ρ(r,t) be its mass density (amount of mass per unit volume) at the same point r. The flux is a vector field (at any point a vector gives the direction of flow), and the density is a scalar field (function). The continuity equation states that
Multiply the left- and right-hand side by an infinitesimal volume element ΔV containing the point r. Then the left hand side gives the mass leaving ΔV minus the mass entering ΔV (per unit time). The right-hand becomes equal to 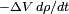 which is the rate of decrease in mass. Hence the net flow of mass leaving the the volume ΔV is equal to the decrease of mass in ΔV (both per unit time).
which is the rate of decrease in mass. Hence the net flow of mass leaving the the volume ΔV is equal to the decrease of mass in ΔV (both per unit time).
If the fluid is incompressible, i.e., the mass density ρ is constant, meaning that its time derivative is zero, the flux satisifies
Such a vector field φ(r,t) is called divergence-free, solenoidal, transverse, or circuital.
Note
From the Helmholtz decomposition of a vector field it follows that a divergence-free vector field can be written as the curl of another vector field, i.e., provided the longitudinal component ∇⋅F = 0, we have
where A is sometimes referred to as the vector potential. A very well-known example of a divergence-free field is a magnetic field B, which is divergence-free by virtue of one of Maxwell's equations. The vector field A is then the magnetic vector potential.