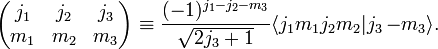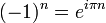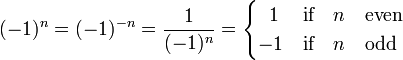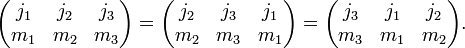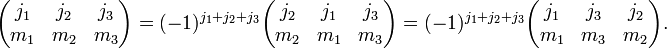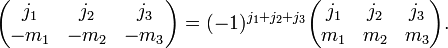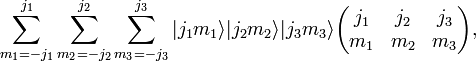3j-symbol

From Knowino

Jump to: navigation, search

In physics and mathematics, Wigner 3-jm symbols, also called 3j symbols, are related to the Clebsch-Gordan coefficients of the groups SU(2) and SO(3) through

$\begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & m_3 \end{pmatrix} \equiv \frac{(-1)^{j_1-j_2-m_3}}{\sqrt{2j_3+1}} \langle j_1 m_1 j_2 m_2 | j_3 \, {-m_3} \rangle.$

The 3j symbols show more symmetry in permutation of the labels than the corresponding Clebsch-Gordan coefficients. Exactly as is true for the Clebsch-Gordan coefficients, the j-values are positive and either integral: (0, 1, 2,..) or half-integral: (1/2, 3/2, 5/2, ...).

Note on phases

All 3j symbols are real, which means that the value of n in overall phase factors of the kind:

$(-1)^n = e^{i\pi n}\;$

must be integral, otherwise exp[iπn] would not be on the real axis in the complex plane. For half-integral n the phase factor is purely imaginary and a 3j symbol containing the factor would be too, so that half-integral values do not appear as powers of −1. The overall powers of −1 are odd or even integral numbers. The following relation (n integral) seems not to be known to everyone contributing to the corresponding article on Wikipedia:

$(-1)^n = (-1)^{-n}= \frac{1}{(-1)^n}= \begin{cases} \;\;1 &\hbox{if}\quad n\quad \hbox{even}\\ -1 &\hbox{if}\quad n\quad \hbox{odd}\\ \end{cases}$

Note that the expression

$j \pm m\quad\hbox{with}\quad -j \le m \le j$

is necessarily integral, since m runs in unit steps and j−m_max = j+m_min =0. Likewise j₁−j₂±m₃ is integral [±m₃ = ±(−m₁−m₂)].

Inverse relation

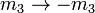
The inverse relation—the Clebsch-Gordan coefficient given by a 3j symbol—can be found by noting that j₁ - j₂ - m₃ is an integral number and making the substitution $m_3 \rightarrow -m_3$

$\langle j_1 m_1 j_2 m_2 | j_3 m_3 \rangle = (-1)^{j_1-j_2+m_3}\sqrt{2j_3+1} \begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & -m_3 \end{pmatrix}.$

Symmetry properties

The symmetry properties of 3j symbols are more convenient than those of Clebsch-Gordan coefficients. A 3j symbol is invariant under an even permutation of its columns:

$\begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & m_3 \end{pmatrix} = \begin{pmatrix} j_2 & j_3 & j_1\\ m_2 & m_3 & m_1 \end{pmatrix} = \begin{pmatrix} j_3 & j_1 & j_2\\ m_3 & m_1 & m_2 \end{pmatrix}.$

An odd permutation of the columns gives a phase factor:

$\begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & m_3 \end{pmatrix} = (-1)^{j_1+j_2+j_3} \begin{pmatrix} j_2 & j_1 & j_3\\ m_2 & m_1 & m_3 \end{pmatrix} = (-1)^{j_1+j_2+j_3} \begin{pmatrix} j_1 & j_3 & j_2\\ m_1 & m_3 & m_2 \end{pmatrix}.$

Changing the sign of the $m$ quantum numbers also gives a phase:

$\begin{pmatrix} j_1 & j_2 & j_3\\ -m_1 & -m_2 & -m_3 \end{pmatrix} = (-1)^{j_1+j_2+j_3} \begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & m_3 \end{pmatrix}.$

Selection rules

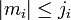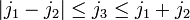The Wigner 3j is zero unless $m 1 + m 2 + m 3 = 0$ , $j 1 + j 2 + j 3$ is integer, $|m_i| \le j_i$ and $|j_1-j_2|\le j_3 \le j_1+j_2$ .

Scalar invariant

The contraction of the product of three rotational states with a 3j symbol,

$\sum_{m_1=-j_1}^{j_1} \sum_{m_2=-j_2}^{j_2} \sum_{m_3=-j_3}^{j_3} |j_1 m_1\rangle |j_2 m_2\rangle |j_3 m_3\rangle \begin{pmatrix} j_1 & j_2 & j_3\\ m_1 & m_2 & m_3 \end{pmatrix},$

is invariant under rotations.

Orthogonality Relations

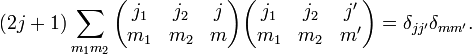
$(2j+1)\sum_{m_1 m_2} \begin{pmatrix} j_1 & j_2 & j\\ m_1 & m_2 & m \end{pmatrix} \begin{pmatrix} j_1 & j_2 & j'\\ m_1 & m_2 & m' \end{pmatrix} =\delta_{j j'}\delta_{m m'}.$

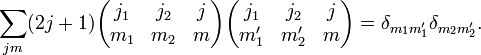
$\sum_{j m} (2j+1) \begin{pmatrix} j_1 & j_2 & j\\ m_1 & m_2 & m \end{pmatrix} \begin{pmatrix} j_1 & j_2 & j\\ m_1' & m_2' & m \end{pmatrix} =\delta_{m_1 m_1'}\delta_{m_2 m_2'}.$

References

E. P. Wigner, On the Matrices Which Reduce the Kronecker Products of Representations of Simply Reducible Groups, unpublished (1940). Reprinted in: L. C. Biedenharn and H. van Dam, Quantum Theory of Angular Momentum, Academic Press, New York (1965).
A. R. Edmonds, Angular Momentum in Quantum Mechanics, 2nd edition, Princeton University Press, Pinceton, 1960.
D. M. Brink and G. R. Satchler, Angular Momentum, 3rd edition, Clarendon, Oxford, 1993.
L. C. Biedenharn and J. D. Louck, Angular Momentum in Quantum Physics, volume 8 of Encyclopedia of Mathematics, Addison-Wesley, Reading, 1981.
D. A. Varshalovich, A. N. Moskalev, V. K. Khersonskii, Quantum Theory of Angular Momentum, World Scientific Publishing Co., Singapore, 1988.

3j-symbol

Contents

Note on phases

Inverse relation

Symmetry properties

Selection rules

Scalar invariant

Orthogonality Relations

References

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox