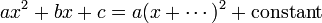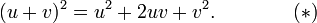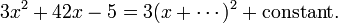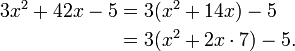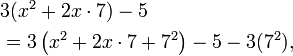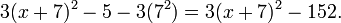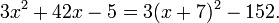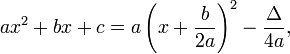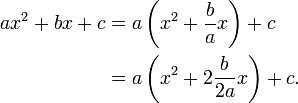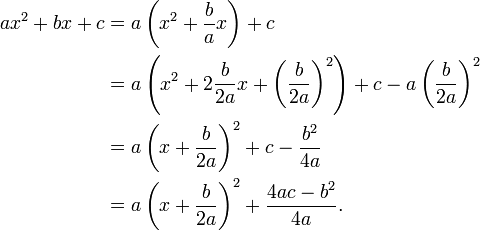Completing the square
In algebra, completing the square is a way of rewriting a quadratic polynomial as the sum of a constant and a constant multiple of the square of a first-degree polynomial. Thus one has
and completing the square is the way of filling in the blank between the brackets. Completing the square is used for solving quadratic equations (the proof of the well-known formula for the general solution consists of completing the square). The technique is also used to find the maximum or minimum value of a quadratic function, or in other words, the vertex of a parabola.
The technique relies on the elementary algebraic identity
Concrete examples
We want to fill in this blank:
We write
Now the expression (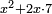 ) corresponds to
) corresponds to 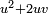 in the elementary identity labeled (*) above. If
in the elementary identity labeled (*) above. If 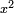 is
is 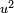 and
and 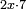 is
is 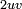 , then
, then  must be 7. Therefore
must be 7. Therefore 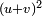 must be
must be 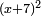 . So we continue:
. So we continue:
Now we have added 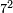 inside the parentheses, and compensated (thus justifying the "=") by subtracting
inside the parentheses, and compensated (thus justifying the "=") by subtracting 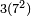 outside the parentheses. The expression inside the parentheses is now
outside the parentheses. The expression inside the parentheses is now 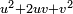 , and by the elementary identity labeled (*) above, it is therefore equal to
, and by the elementary identity labeled (*) above, it is therefore equal to 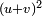 , i.e. to
, i.e. to 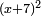 . So now we have
. So now we have
Thus we have the equality
More abstractly
It is possible to give a closed formula for the completion in terms of the coefficients a, b and c. Namely,
where 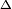 stands for the well-known discriminant of the polynomial, that is
stands for the well-known discriminant of the polynomial, that is 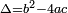 .
.
Indeed, we have
The last expression inside parentheses above corresponds to 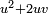 in the identity labelled (*) above. We need to add the third term,
in the identity labelled (*) above. We need to add the third term, 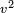 :
:
| |
Some content on this page may previously have appeared on Citizendium. |