Complex conjugation
From Knowino
This is a pending revision of this page. It may differ from the latest accepted revision, which was accepted on 13 January 2011.
In mathematics, complex conjugation is an operation on complex numbers which reverses the sign of the imaginary part, that is, it sends z = x + iy to the complex conjugate 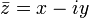 .
.
In the geometrical interpretation in terms of the Argand diagram, complex conjugation is represented by reflection in the x-axis. The complex numbers left fixed by conjugation are precisely the real numbers.
Conjugation respects the algebraic operations of the complex numbers: 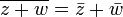 and
and 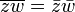 . Hence conjugation represents an automorphism of the field of complex numbers over the field of real numbers, and is the only non-trivial automorphism. One can say it is impossible to tell which is i and which is -i.
. Hence conjugation represents an automorphism of the field of complex numbers over the field of real numbers, and is the only non-trivial automorphism. One can say it is impossible to tell which is i and which is -i.
| |
Some content on this page may previously have appeared on Citizendium. |

