Basis (linear algebra)
In linear algebra, a basis for a vector space V is a set of vectors in V such that every vector in V can be written uniquely as a finite linear combination of vectors in the basis. One may think of the vectors in a basis as building blocks from which all other vectors in the space can be assembled. This is similar to viewing the prime numbers as building blocks from which positive integers can be assembled.
Every nonzero vector space has a basis, and in fact, infinitely many different bases. This result is of paramount importance in the theory of vector spaces, in the same way that the unique factorization theorem is of fundamental importance in the study of integers. For instance, the existence of a finite basis for a vector space provides the space with an invertible linear transformation to Euclidean space, given by taking the coordinates of a vector with respect to a basis. Through this transformation, every finite dimensional vector space can be considered to be essentially "the same as" the space 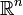 just with different labels for the vectors and operations. (Here,
just with different labels for the vectors and operations. (Here, 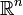 consists of row vectors
consists of row vectors 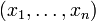 with n real number entries.)
with n real number entries.)
If a vector space has a finite basis, then every basis for the space has the same number of elements: this number is the dimension of the space.
The term basis is also used in abstract algebra, specifically in the theory of free modules. For more on this use of the term, see the advanced subpage.
Examples
- The plane
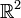 has a standard basis often denoted by i and j, unit vectors along the x and y axes respectively. However, there are many other possible bases such as i+j and i-j, or 2i+3j and 4i-5j.
has a standard basis often denoted by i and j, unit vectors along the x and y axes respectively. However, there are many other possible bases such as i+j and i-j, or 2i+3j and 4i-5j.
- The set of solutions to the differential equation y'' = − y is a vector space with a basis consisting of the two functions y = sin(x) and y = cos(x). Again there are other possible bases, for example the shifted functions y = sin(x + α) and y = cos(x + α) for any phase angle α.
- The polynomials in a variable x form a vector space. One basis for this space is the set of all powers ("monomials"),
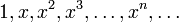 . Although there are infinitely many elements in this basis, each polynomial can be expressed uniquely as a combination of only finitely many powers: indeed, this is how a polynomial is defined.
. Although there are infinitely many elements in this basis, each polynomial can be expressed uniquely as a combination of only finitely many powers: indeed, this is how a polynomial is defined.
| |
Some content on this page may previously have appeared on Citizendium. |