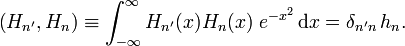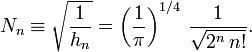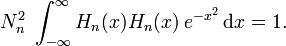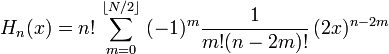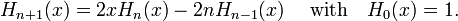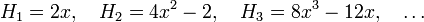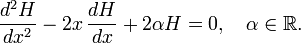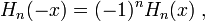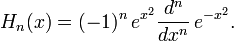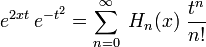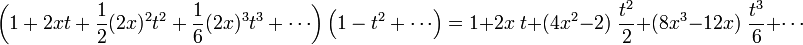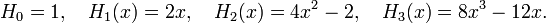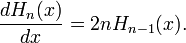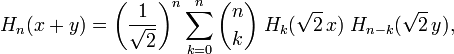Hermite polynomial
Contents |
In mathematics and physics, Hermite polynomials form a well-known class of orthogonal polynomials. In quantum mechanics they appear as eigenfunctions of the harmonic oscillator and in numerical analysis they play a role in Gauss-Hermite quadrature. The functions are named after the French mathematician Charles Hermite (1822–1901).
- See Addendum for a table of Hermite polynomials through n = 12.
[edit] Orthonormality
The Hermite polynomials Hn(x) are orthogonal in the sense of the following inner product:
That is, the polynomials are defined on the full real axis and have weight w(x) = exp(−x²). Their orthogonality is expressed by the appearance of the Kronecker delta δn'n. The normalization constant is given by
Normalization is to unity
The polynomials NnHn(x) are orthonormal, which means that they are orthogonal and normalized to unity.
[edit] Explicit expression
here 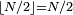 if N even and
if N even and 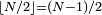 if N odd.
if N odd.
[edit] Recursion relation
Orthogonal polynomials can be constructed recursively by means of a Gram-Schmidt orthogonalization procedure. This procedure yields the following relation
The first few follow immediately from this relation,
[edit] Differential equation
The polynomials Hn(x) satisfy the Hermite differential equation
for the special case 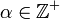 , i.e., for natural positive α.
, i.e., for natural positive α.
- If α ≡ n is even, the solution is a polynomial of order n consisting of even powers of x only.
- If α ≡ n is odd, the solution is a polynomial of order n consisting of odd powers of x only.
[edit] Symmetry
the functions of even n are symmetric under x → −x and those of odd n are antisymmetric under this substitution.
[edit] Rodrigues' formula
[edit] Generating function
First few terms
so that
[edit] Differential relation
[edit] Sum formula
where  is a binomial coefficient.
is a binomial coefficient.
[edit] References
M. Abramowitz and I.A. Stegun (Eds), Handbook of Mathematical Functions, Dover, New York (1972). Chapter 22
Eric W. Weisstein, Hermite Polynomial