Almost sure convergence
Almost sure convergence is one of the four main modes of stochastic convergence. It may be viewed as a notion of convergence for random variables that is similar to, but not the same as, the notion of pointwise convergence for real functions.
[edit] Definition
In this section, a formal definition of almost sure convergence will be given for complex vector-valued random variables, but it should be noted that a more general definition can also be given for random variables that take on values on more abstract topological spaces. To this end, let 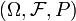 be a probability space (in particular,
be a probability space (in particular, 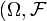 ) is a measurable space). A (
) is a measurable space). A (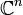 -valued) random variable is defined to be any measurable function
-valued) random variable is defined to be any measurable function 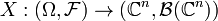 , where
, where 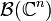 is the sigma algebra of Borel sets of
is the sigma algebra of Borel sets of 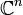 . A formal definition of almost sure convergence can be stated as follows:
. A formal definition of almost sure convergence can be stated as follows:
A sequence 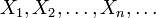 of random variables is said to converge almost surely to a random variable Y if
of random variables is said to converge almost surely to a random variable Y if 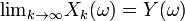 for all
for all 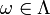 , where
, where 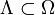 is some measurable set satisfying P(Λ) = 1. An equivalent definition is that the sequence
is some measurable set satisfying P(Λ) = 1. An equivalent definition is that the sequence 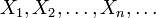 converges almost surely to Y if
converges almost surely to Y if 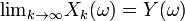 for all
for all 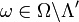 , where Λ' is some measurable set with P(Λ') = 0. This convergence is often expressed as:
, where Λ' is some measurable set with P(Λ') = 0. This convergence is often expressed as:
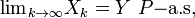
or
 .
.
[edit] Important cases of almost sure convergence
If we flip a coin n times and record the percentage of times it comes up heads, the result will almost surely approach 50% as 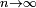 .
.
This is an example of the strong law of large numbers.
| |
Some content on this page may previously have appeared on Citizendium. |

