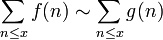Average order of an arithmetic function
From Knowino
In mathematics, in the field of number theory, the average order of an arithmetic function is some simpler or better-understood function which takes the same values "on average".
Let f be a function on the natural numbers. We say that the average order of f is g if
as x tends to infinity.
It is conventional to assume that the approximating function g is continuous and monotone.
[edit] Examples
- The average order of d(n), the number of divisors of n, is log(n);
- The average order of σ(n), the sum of divisors of n, is
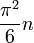 ;
;
- The average order of φ(n)), Euler's totient function of n, is
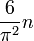 ;
;
- The average order of r(n)), the number of ways of expressing n as a sum of two squares, is π ;
- The Prime Number Theorem is equivalent to the statement that the von Mangoldt function Λ(n) has average order 1.
[edit] See also
[edit] References
- G.H. Hardy; E.M. Wright (2008). An Introduction to the Theory of Numbers, 6th ed.. Oxford University Press, 347-360. ISBN 0-19-921986-5.
- Gérald Tenenbaum (1995). Introduction to Analytic and Probabilistic Number Theory. Cambridge University Press, 36-55. ISBN 0-521-41261-7.
| |
Some content on this page may previously have appeared on Citizendium. |