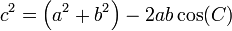Law of cosines
From Knowino
In geometry the law of cosines is a useful identity for determining an angle or the length of one side of a triangle when given either two angles and three lengths or three angles and two lengths. When dealing with a right triangle, the law of cosines reduces to the Pythagorean theorem because of the fact that cos(90°)=0. To determine the areas of triangles, see the law of sines. The law of cosines can be stated as
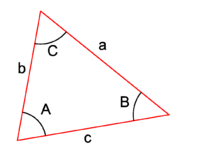
where a, b, and c are the lengths of the sides of the triangle opposite to angles A, B, and C, respectively (see Figure 1).
| |
Some content on this page may previously have appeared on Citizendium. |