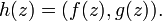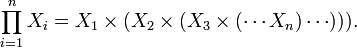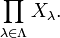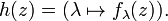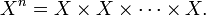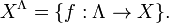Cartesian product
In mathematics, the Cartesian product of two sets X and Y is the set of ordered pairs from X and Y: it is denoted 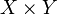 or, less often,
or, less often,  .
.
There are projection maps pr1 and pr2 from the product to X and Y taking the first and second component of each ordered pair respectively.
The Cartesian product has a universal property: if there is a set Z with maps 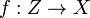 and
and  , then there is a map
, then there is a map 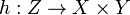 such that the compositions
such that the compositions 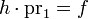 and
and 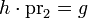 . This map h is defined by
. This map h is defined by
[edit] General products
The product of any finite number of sets may be defined inductively, as
The product of a general family of sets Xλ as λ ranges over a general index set Λ may be defined as the set of all functions x with domain Λ such that x(λ) is in Xλ for all λ in Λ. It may be denoted
The Axiom of Choice is equivalent to stating that a product of any family of non-empty sets is non-empty.
There are projection maps prλ from the product to each Xλ.
The Cartesian product has a universal property: if there is a set Z with maps 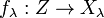 , then there is a map
, then there is a map 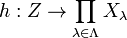 such that the compositions
such that the compositions 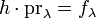 . This map h is defined by
. This map h is defined by
[edit] Cartesian power
The n-th Cartesian power of a set X is defined as the Cartesian product of n copies of X
A general Cartesian power over a general index set Λ may be defined as the set of all functions from Λ to X
[edit] References
- Paul Halmos (1960). Naive set theory. Van Nostrand Reinhold, 24.
- Keith J. Devlin (1979). Fundamentals of Contemporary Set Theory. Springer-Verlag, 12. ISBN 0-387-90441-7.
| |
Some content on this page may previously have appeared on Citizendium. |