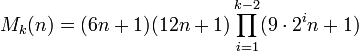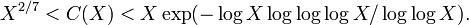Carmichael number
A Carmichael number is a composite number named after the mathematician Robert Daniel Carmichael. A Carmichael number  divides
divides 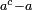 for every integer
for every integer  . A Carmichael number c also satisfies the congruence
. A Carmichael number c also satisfies the congruence  , if
, if 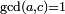 . The first few Carmichael numbers are 561, 1105, 1729, 2465, 2821, 6601 and 8911. In 1994 Pomerance, Alford and Granville proved that there exist infinitely many Carmichael numbers.
. The first few Carmichael numbers are 561, 1105, 1729, 2465, 2821, 6601 and 8911. In 1994 Pomerance, Alford and Granville proved that there exist infinitely many Carmichael numbers.
Contents |
Properties
- Every Carmichael number is square-free and has at least three different prime factors
- For every Carmichael number c it holds that c − 1 is divisible by pn − 1 for every one of its prime factors pn.
- Every absolute Euler pseudoprime is a Carmichael number.
Chernick's Carmichael numbers
J. Chernick found in 1939 a way to construct Carmichael numbers[1]
[2]. If, for a natural number n, the three numbers 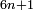 ,
, 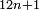 and
and 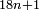 are prime numbers, the product
are prime numbers, the product 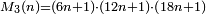 is a Carmichael number. This condition can only be satisfied if the number
is a Carmichael number. This condition can only be satisfied if the number 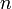 ends with 0, 1, 5 or 6. An equivalent formulation of Chernick's construction is that if
ends with 0, 1, 5 or 6. An equivalent formulation of Chernick's construction is that if 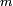 ,
, 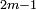 and
and 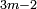 are prime numbers, then the product
are prime numbers, then the product 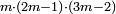 is a Carmichael number.
is a Carmichael number.
This way to construct Carmichael numbers may be extended[3] to
with the condition that each of the factors is prime and that 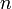 is divisible by 2k − 4.
is divisible by 2k − 4.
Distribution of Carmichael numbers
Let C(X) denote the number of Carmichael numbers less than or equal to X. Then for all sufficiently large X
The upper bound is due to Erdős(1956)[4] and Pomerance, Selfridge and Wagstaff (1980)[5] and the lower bound is due to Alford, Granville and Pomerance (1994)[6]. The asymptotic rate of growth of C(X) is not known.[7]
References and notes
- ↑ J. Chernick, "On Fermat's simple theorem", Bull. Amer. Math. Soc. 45 (1939) 269-274
- ↑ (2003-11-22) Generic Carmichael Numbers
- ↑ Paulo Ribenboim, The new book of prime number records, Springer-Verlag (1996) ISBN 0-387-94457-5. P.120
- ↑ Paul Erdős, "On pseudoprimes and Carmichael numbers", Publ. Math. Debrecen 4 (1956) 201-206. MR 18 18
- ↑ C. Pomerance, J.L. Selfridge and S.S. Wagstaff jr, "The pseudoprimes to 25.109", Math. Comp. 35 (1980) 1003-1026. MR 82g:10030
- ↑ W. R. Alford, A. Granville, and C. Pomerance. "There are Infinitely Many Carmichael Numbers", Annals of Mathematics 139 (1994) 703-722. MR 95k:11114
- ↑ Richard Guy, "Unsolved problems in Number Theory" (3rd ed), Springer-Verlag (2004) ISBN 0-387-20860-7. Section A13
| |
Some content on this page may previously have appeared on Citizendium. |