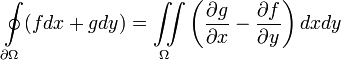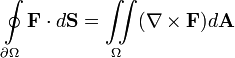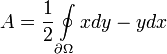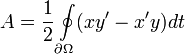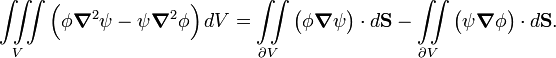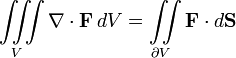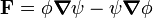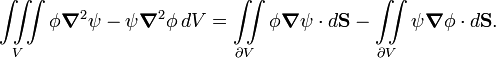Green's Theorem
Green's Theorem is a vector identity that is equivalent to the curl theorem in two dimensions. It relates the line integral around a simple closed curve 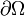 with the double integral over the plane region
with the double integral over the plane region 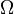 .
.
The theorem is named after the British mathematician George Green. It can be applied to various fields in physics, among others flow integrals.
Contents |
Mathematical Statement in two dimensions
Let 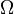 be a region in
be a region in 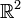 with a positively oriented, piecewise smooth, simple closed boundary
with a positively oriented, piecewise smooth, simple closed boundary 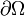 . f(x,y) and g(x,y) are functions defined on a open region containing
. f(x,y) and g(x,y) are functions defined on a open region containing 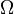 and have continuous partial derivatives in that region. Then Green's Theorem states that
and have continuous partial derivatives in that region. Then Green's Theorem states that
The theorem is equivalent to the curl theorem in the plane and can be written in a more compact form as
Application: Area Calculation
Green's theorem is very useful when it comes to calculating the area of a region. If we take f(x,y) = y and g(x,y) = x, the area of the region 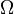 , with boundary
, with boundary 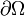 can be calculated by
can be calculated by
This formula gives a relationship between the area of a region and the line integral around its boundary.
If the curve is parametrized as 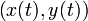 , the area formula becomes
, the area formula becomes
Statement in three dimensions
Different ways of formulating Green's theorem in three dimensions may be found. One of the more useful formulations is
Proof
The divergence theorem reads
where 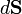 is defined by
is defined by 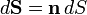 and
and 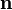 is the outward-pointing unit normal vector field.
is the outward-pointing unit normal vector field.
Insert
and use
so that we obtain the result to be proved,
| |
Some content on this page may previously have appeared on Citizendium. |