Cofactor (mathematics)
In mathematics, a cofactor appears in the definition of the determinant of a square matrix.
Let M be a square matrix of size n. The (i,j) minor refers to the determinant of the (n-1)×(n-1) submatrix Mi,j formed by deleting the i-th row and j-th column from M (or sometimes just to the submatrix Mi,j itself). The corresponding cofactor is the signed minor
The adjugate matrix adj M (in older literature called adjoint matrix[1]) is the n×n matrix whose (i,j) entry is the (j,i) cofactor (note the transposition of the indices). Letting In be the n×n identity (unit) matrix, we have
which encodes the rule for expansion of the determinant of M by any the cofactors of any row or column. This expression shows that if det(M) is non-zero, then M is invertible and its inverse is the following,
A proof of this equation may be found in this article.
[edit] Example
Consider the following example matrix,
Its minors are the determinants (vertical bars indicate a determinant):
The adjugate matrix of M is
and the inverse matrix is
Indeed,
and the other matrix elements of the product follow likewise.
[edit] Note
- ↑ The term "adjoint" for the adjugate matrix is disappearing because it is felt that it is easily confused with Hermitian adjoint, the transpose and complex conjugate of a matrix.
[edit] References
- C.W. Norman (1986). Undergraduate Algebra: A first course. Oxford University Press, 306,310,315. ISBN 0-19-853248-2.
| |
Some content on this page may previously have appeared on Citizendium. |
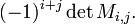
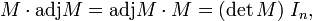
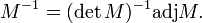
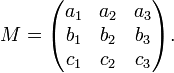
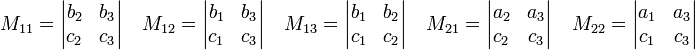
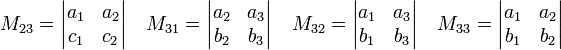
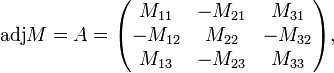
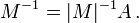
![\begin{align}
\left( M\; M^{-1}\right)_{11} & = |M|^{-1}\left( a_1 M_{11}- a_2 M_{12} + a_3 M_{13}\right) = \frac{|M|}{|M|} = 1 \\
\left( M\; M^{-1}\right)_{21} & = |M|^{-1}\left( b_1 M_{11}- b_2 M_{12} + b_3 M_{13}\right)
=|M|^{-1}\left[ b_1(b_2c_3-b_3c_2) - b_2(b_1c_3-b_3c_1) + b_3(b_1c_2-b_2c_1)\right] = 0 ,\\
\end{align}](images/math/8/3/4/834fb6f03da68aacdf229609c99873f1.png)