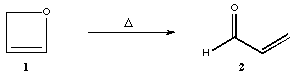
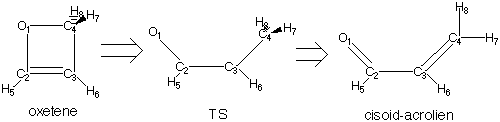
Mapping the Potential Energy Surface for the Ring Opening Reaction of Protonated

Mapping the potential energy surface for the thermal ring opening

reaction of oxetene to form cisoid-acrolein

(Gaussian 98 & GaussView)

Mapping the potential energy surface for a chemical reaction involves locating the reactants, the products, the intermediates, and the transition state geometries. With a complete map, it is possible define the detailed reaction mechanism theoretically and to predict the enthalpies and the free energies of activation and reaction.

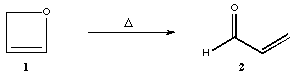
In this exercise, you will theoretically explore the potential energy surface for a single-step reaction, the ring opening reaction of oxetene (1) to cisoid-acrolein (2).

You will also learn several methods for computationally exploring a reaction mechanism. You will use Gaussian 98 as your computational software and GaussView as visual aids for generating Gaussian scripts, visualizing vibrational frequencies and output geometries, and following the reaction path from the transition state structure back to the reactant and forward to the product.

This exercise has the following outline:

Step 1. Locating the minima (reactant and product):

Create geometries of reactant and product with GaussView.
Performing full geometry optimizations and vibrational frequency calculations.

Step 2. Locating the transition state:

Performing TS search to find the transition state structure.
Calculating the vibrational frequencies for the transition state (NImag = 1).

Step 3. Following the reaction path from the transition state to the reactant and product:

Performing Intrinsic Reaction Coordinate (IRC) search in 2 directions to link the transition state structure to the reactant and the product, to confirm that the transition state located actually leads to the expected reactant and product.

Step 4. Drawing the energy profile of the reaction

***********************************************************************************************

Step 1. Locating the Minima:

In this section, you will model the reactant and the product by performing a full geometry optimization and frequency calculation on each.

Drawing the structures of reactant and product with GaussView:

Ensure that the structures you draw are not symmetric, otherwise Gaussian will not find the correct minimum geometry of your molecule. You can do this by changing the angles of some H atoms and the dihedral angle of double bonds.

Performing geometry optimizations and vibrational frequency calculations for each compound:

Submit the drawn structure of your compound to Gaussian, at the RHF/6-31G(d) level of theory (Jobtype: optimization). Write down the calculated energy E(RHF) and check if your optimized structure is really a minimum by making a frequency analysis. You can do this by submitting a job (Jobtype: frequency) for your optimized structure to Gaussian.

Results:

1. After the Gaussian jobs are completed, check the number of imaginary frequencies by searching for the "NImag= " term. Make sure that you get "NImag=0", for your minima. The NImag expression is in the archive part, at the end of the .log file.

2. You can also check the results graphically in GaussView by opening your log file and click the option 'Vibrations' in the 'Results' menu.

***Note: In this exercise make sure that oxetene and cisoid-acrolein have Cs symmetry. The point group symmetry is reported in the archive part of the .log files, as "P0G= " immediately before NImag.

*************************************************************************************************

Step 2. Locating the Transition State:

After locating the minima, you should locate the transition state structure that connects them. One way to do this is with a transition state (TS) search.

Performing a Transition State search:

In this part, you must start by guessing the structure of your transition state and you will find the energy of the actual transition state structure. Transition state searching methods may be thought of as the usual geometry optimizations for minima, but in the opposite direction (upward in energy toward a saddle point). The search is conducted for a structure that is a maximum in one, and only one dimension, and a minimum in all the other [(3N-6) -1] dimensions (a first-order saddle point). The maximum energy dimension is associated with the vibration with 1 negative (imaginary) frequency, reported in the .log file after the frequency calculation on the optimized transition state.

Draw a guess structure of your TS in GaussView (hint: take the optimized geometry of oxetene as a start and make the distances between all the carbon atoms and oxygen longer). Submit your drawn structure to Gaussian with the following options:

1) RHF/6-31G(d)

2) Jobtype: optimization

3) Calculate force constants initially

4) Locate transition state

5) Additional keywords: OPT=NOEIGENTEST

Checking the TS by calculating the vibrational frequencies for the transition state:

Having calculated the geometry of the transition state, you will need to check if this structure is really the transition state. You can do this by finding its vibrational frequencies in the following way:

The input geometry for this computation is the output geometry of the TS search. To obtain this geometry you can open the TS logfile in GaussView. Submit it to Gaussian with the following options:

1) RHF/6-31G(d)

2) Jobtype: frequency

Results from your final TS Calculation and frequency job:

1. Check the "NImag= #" term in the .log file. The Nimag expression is in the archive part, at the end of the .log file. Remember, here you want to have one imaginary frequency.

2. Visualize the geometry and the atomic motions for the imaginary vibrational frequency using GaussView and see if it corresponds to the motions required for the mechanistic scheme. By visualizing the motions for the negative frequency you can see the motion along the reaction coordinate taking you to reactants and products. Write down the E(RHF) of your calculated transition state.

*************************************************************************************************

Step 3. Following the reaction path from the transition state to the reactant and product:

This part serves as a test for making sure that the transition state located actually connects the desired reactant and product. The IRC search moves along the reaction path (reaction coordinate) by initially reading the force constants from the frequency calculation made for the transition state and contained in the checkpoint file. The program then follows the steepest descent path along the path of the negative frequency coordinate to reach the two minima connected by the transition state structure. In this part of the exercise you will perform the IRC searches, and then optimize the geometries of the IRC output structures of the reactant and the product to see if you indeed reach the two structures from Step 1 of this exercise for the expected reactant and product.

Submitting a job for an IRC search:

* The direction for searching is indicated with the keywords "forward" and "reverse".

** In order to have the IRC search proceed in forward and reverse directions, you need to perform one search in each direction. Therefore you need to submit twice the TS structure from the previous TS search part, one time for each direction. In order to do this, you must open the log file of your TS search (not your frequency analysis job!!) in GaussView. Save the structure as a gjf file with a filename which contains 'forward'. Submit this file to Gaussian with the following options:

1) RHF/6-31G(d)

2) Jobtype: IRC

3) Follow IRC oneway, forward

4) Compute more points 20

5) Calculate initial force constants

Do this again with "reverse".

* After the searches are complete, you can watch your final structure in GaussView by opening the .log file.

**It's possible that Gaussian immediately gives an error after submitting the file. Gaussian is then probably using the wrong .chk file for this job. This can be solved by recalculating the TS or by removing all .chk files in the scratch directory of Gaussian.

***The IRC search will not necessarily reach the minimum. In order to complete the reaction path to minima, perform a final geometry optimization and frequency calculation for each minimum, with the starting structure being the output structure of the IRC runs. This can be done by taking the final geometry of each IRC search, and submitting a geometry optimization (as in step 1).

After the final geometry optimization are complete, open the logfiles using GaussView, to see if these two minima are indeed those of the expected reactant and product from that transition state.

************************************************************************************************

Step 4. Drawing the energy profile of the reaction

To draw the energy profile of the reaction you need the E(RHF) energies and the Free energies (DG) which are reported in the .log files from the last runs of the steps 1 and 2. The energies reported in the .log file are in atomic units or Hartrees. You must convert them into kcal/mol (multiply with 627.51). Draw the energy of your reaction profile and draw also the Gibbs Free energy. (hint: It is best to set the energy of the product cisoid-acrolein to zero and calculate the energies of the reactant oxetene and the TS relative to the product energy.

Complete the following table with the values reported in the .log files:

TABLE 1

Oxetene (1) TS Cisoid-acrolein (2)

E(RHF) . . .

DG (kcal/mol) . . .

TABLE 1
	Oxetene (1)	TS	Cisoid-acrolein (2)
E(RHF)	.	.	.
DG (kcal/mol)	.	.	.