Next: C..14 CS1: Colle-Salvetti correlation
Up: C. Density functional descriptions
Previous: C..12 BRUEG: Becke-Roussel Exchange
C..13 BW: Becke-Wigner Exchange-Correlation Functional
Hybrid exchange-correlation functional comprimising Becke's 1998 exchange and Wigner's spin-polarised correlation functionals.
See reference [14] for more details.
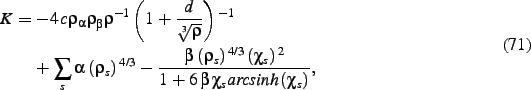 where
where
![\begin{dmath}
\alpha=-3/8\,\sqrt [3]{3}{4}^{2/3}\sqrt [3]{{\pi }^{-1}}
,\end{dmath}](img682.gif)

 and
and
 To avoid singularities in the limit
To avoid singularities in the limit
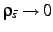
molpro@molpro.net
Oct 10, 2007
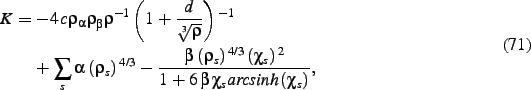 where
where
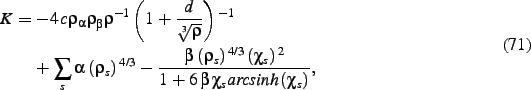 where
where
![]()
![]()
![]() and
and
![]() To avoid singularities in the limit
To avoid singularities in the limit
![]()
![]()