Next: C..9 B97R: Density functional
Up: C. Density functional descriptions
Previous: C..7 B88: Becke88 Exchange
C..8 B95: Becke95 Correlation Functional
 dependent Dynamical correlation functional.
See reference [12] for more details.
dependent Dynamical correlation functional.
See reference [12] for more details.
 where
where
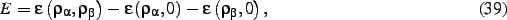




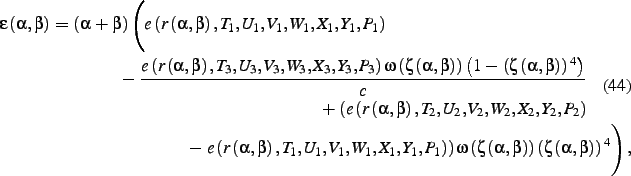
![\begin{dmath}
r \left( \alpha,\beta \right) =1/4\,\sqrt [3]{3}{4}^{2/3}\sqrt [3]{{
\frac {1}{\pi \, \left( \alpha+\beta \right) }}}
,\end{dmath}](img647.gif)

![\begin{dmath}
\omega \left( z \right) ={\frac { \left( 1+z \right) ^{4/3}+ \left( 1-z
\right) ^{4/3}-2}{2\,\sqrt [3]{2}-2}}
,\end{dmath}](img649.gif)
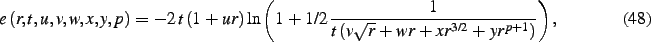

![\begin{dmath}
T
=
[ 0.031091, 0.015545, 0.016887]
,\end{dmath}](img652.gif)
![\begin{dmath}
U
=
[ 0.21370, 0.20548, 0.11125]
,\end{dmath}](img653.gif)
![\begin{dmath}
V
=
[ 7.5957, 14.1189, 10.357]
,\end{dmath}](img654.gif)
![\begin{dmath}
W
=
[ 3.5876, 6.1977, 3.6231]
,\end{dmath}](img655.gif)
![\begin{dmath}
X
=
[ 1.6382, 3.3662, 0.88026]
,\end{dmath}](img656.gif)
![\begin{dmath}
Y
=
[ 0.49294, 0.62517, 0.49671]
\end{dmath}](img657.gif) and
and
![\begin{dmath}
P
=
[1,1,1]
.\end{dmath}](img658.gif) To avoid singularities in the limit
To avoid singularities in the limit
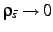

molpro@molpro.net
Oct 10, 2007
 where
where
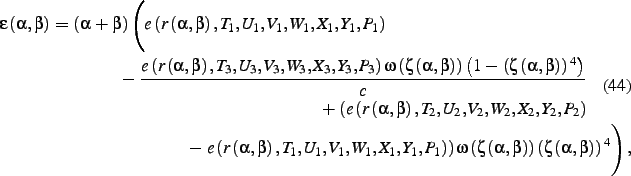
![\begin{dmath}
r \left( \alpha,\beta \right) =1/4\,\sqrt [3]{3}{4}^{2/3}\sqrt [3]{{
\frac {1}{\pi \, \left( \alpha+\beta \right) }}}
,\end{dmath}](img647.gif)
 where
where
![]()
![]()
![]()
![]()
![]()
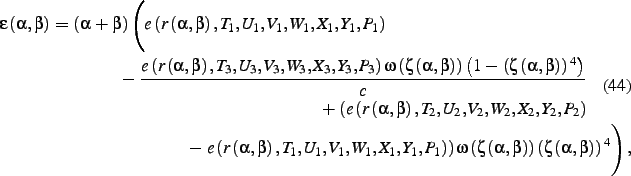
![\begin{dmath}
r \left( \alpha,\beta \right) =1/4\,\sqrt [3]{3}{4}^{2/3}\sqrt [3]{{
\frac {1}{\pi \, \left( \alpha+\beta \right) }}}
,\end{dmath}](img647.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() and
and
![]() To avoid singularities in the limit
To avoid singularities in the limit
![]()
![]()