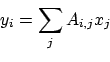Rekenen met matrices en vectoren

Een belangrijk voordeel van MATLAB is dat je heel eenvoudig met matrices en vectoren kunt werken. Een lineaire combinatie

$${\bf c}= 2 {\bf a}+ 3 {\bf b}$$ (1)

wordt berekend met

   c = 2*a +  3*b

We hebben al gezien hoe je een matrix in kunt voeren door alle elementen te geven. De kolommen van een matrix zijn op te vatten als vectoren. Je kunt (kolom) vectoren die even lang zijn samenvoegen tot een matrix door ze naast elkaar te zetten

   C = [ a b ]

Vraagje: wat gebeurt er in dit statement:

   C2 = [ a' ; b' ]'

Nu we weten hoe we vectoren naast elkaar in een matrix kunnen zetten kunnen we gebruik maken van het matrix-vector product om een lineaire combinatie van vectoren te berekenen:

   x = [2; 3]
   c = C * x

Ter herinnering: een matrix-vector product

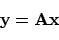$${\bf y}= {\bf A}{\bf x}$$ (2)

is gedefinieerd door

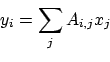$$y_i = \sum_j A_{i,j} x_j$$ (3)

Je kunt de elementen van een matrix er weer uit halen met

   c11 = C(1,1)
   c21 = C(2,1)

enz. Je kunt ook een hele kolom tegelijk uit een matrix halen:

   a2 = C(:,1)
   b2 = C(:,2)

Dit is eigenlijk een verkorte notatie van

   b2 = C(1:end,2)

Omdat in dit geval de matrix drie rijen heeft is dit hetzelfde als

   b2 = C(1:3,2)

waarbij 1:3 een verkorte notatie is van [1 2 3]. Je kan deze index-vector ook eerst in een variabele stoppen

   ind = 1:3
   b2  = C(ind,2)

Deze notatie is op een logische manier uit te breiden, probeer b.v.

   D = C([1 3],:)